In machine learning, Recurrent Neural Network (RNN) is used to predict data that happens one after another. The data has a time element i.e. it has a sequence/order. For example: a video. A video is a series of images arranged in a particular order. Stock prices is also data of this kind, it happens day after day, in sequence (or second after second). Document is also a sequential data, the words are arranged in a particular sequence.
Let’s say we have a video of a dog running, and we try to classify whether the dog in the video jumps or not. So the output is say 100 frames of images, and the output is a binary number, 1 means jump and 0 means not jump, like below (image source: link).

The Recurrent Neural Network receives 100 images as input, one image at a time, in a particular order. And the output is binary number 1 or 0. So it’s a binary classification.
So that’s the input and output of RNN. The input is a sequence of images or numbers (or words), and the output is … well, there are a few different kinds actually:
- One output (like above) i.e. we just take the last output.
- Many output, i.e. we take the output on many different times.
- Generator, e.g. based on 1 note we generate a song.
- #1 above followed by #3 (called encoder-decoder), e.g. Gmail Smart Compose (link).
Architecture
In the early days the RNN architecture was similar to the neural network architecture. See below: input x1 (the first image or number) was fed through a series of neural network layers until we get output y1. Input x2 (the second image or number) was fed through a series of neural network layers until we get output y2, like this:
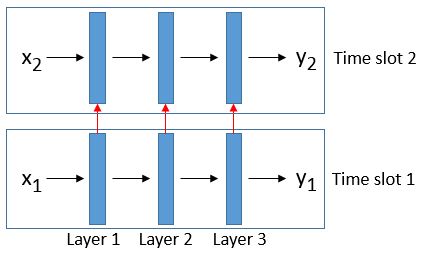
The difference to a normal neural network was the red arrows above, i.e. the values on the hidden layers from time slot 1 was fed to time slot 2. So each layers on time slot 2 received two inputs: x2 and the values of the hidden layers in time slot 1 (multiplied by some weights).
If we take just 1 node in a layer, we can show what happens in this node across time (below left). The node (s) receives input (x) producing output (h). The state of the node (s) is multiplied by a weight ( w ) and sent to itself (s).

The left diagram is simplified into the right diagram above, i.e. we only draw 1 copy, with a circular w from s pointing to itself. The right diagram is called the “rolled” version, and the left one is the “unrolled” version.
Note that in the diagram above the output is h not y, because it is the output of a node in a layer, not the final output of the last layer.
I saw the rolled versions of the RNN diagram above for the first time about 2 years ago and I no idea what it was. I hope you can understand it now.
Long Short Term Memory (LSTM)
These days no one use this original RNN architecture any more. Today everyone uses some variant of LSTM, which looks like this:

This architecture is called Long Short Term Memory because it is using many short term memory cells to create a long term memory (link), meaning: able to remember a long sequence of input, e.g. 5 years of historical stock data. The old RNN inherently has a problem with long sequences because of “vanishing gradient” problem (link). “Exploding gradient” problem (link) is not as big an issue because we can cap it (called “gradient clipping”).
Cell Memory
On the LSTM diagram, the horizontal line at the top (from ct-1 to ct) is the cell state.
It is the memory of the cell i.e. the short term memory. Along this line, there are 3 things happening: the cell state is multiplied by the “forget gate”, increased/reduced by the “input gate” and finally the value is taken to the “output gate”.

So what are these 3 gates? Let’s go through them one by one.
Forget Gate
The forget gate removes unwanted information from the cell state.
The value of σ is from 0 to 1. By varying the value of σ we can adjust how much information is removed from the cell state. The current input (xt) and the previous output (ht-1) are multiplied by σ.

So the impact of this forget gate to the cell state is:

where bf is the bias and Wf and Uf are the weights (link). The blue circle with cross is element wise multiplication.
Bear in mind that t is the current time slot and t-1 is the previous time slot. Notice that h and x have their own weights.
Input Gate
The input gate adds new information into the cell state. As we can see below, the current input (xt) and the previous output (ht-1) pass through a sigma gate and a tanh gate, multiplied then added to the cell memory line.

Here i controls the how much a influences c. The value of tanh is between -1 and +1 so a can decrease or increase c. And the amount of a’s influence to c is controlled by i.
So the impact of this input gate to the cell state is: (link)

Notice that h and x have their own weights, both for i and a.
Output Gate
The output (h) is taken from the cell state (c) using tanh function. The value of tanh is from -1 to +1 so it can make the cell state positive or negative. The amount of influence this tanh(c) has on h is controlled by o. O is calculated from the previous output (ht-1) and the current input (xt), each having different weights, using a sigma function.

So the output (h) is calculated like this:

The complete equation is on Wikipedia: link, which is from Hochreiter and Schidhuber’s original LSTM paper (link) and Gers, Schmidhuber, Cummins’ paper: Learning to forget (link).
A variant of LSTM is Gated Recurrent Unit (GRU). GRU does not have an output gate like LSTM. It has a reset gate and an update gate: link.
Reference:
- Wikipedia, RNN: link
- Wikipedia, LSTM: link
- Wikipedia, GRU: link
- Andrej Karpathy, The Unreasonable Effectiveness of RNN: link
- Michael Phi, Illustrated Guide to LSTM and GRU: link
- Christopher Olah, Understanding LSTM: link
- Gursewak Singh, Demystifying LSTM weights and bias dimensions, link
- Shipra Saxena, Introduction to LSTM: link
- Gu, Gulcehre, Paine, Hoffman, Pascanu, Improving Gating Mechanism in RNN: link
- Hochreiter and Schmidhuber, LSTM: link
Leave a comment